[Keras] Categorical_crossentrophy와 Sparse_categorical_crossentrophy

 - 케라스에서 Categorical_crossentrophy와 Sparse_categorical_crossentrophy 를 손실할수로 쓰겠지만, 두개의 차이는 엄연히 다르니 구분을 잘 해주어야 한다.

 

- 먼저 Keras의 Loss 함수에서는 여러가지 인수들이 주어지는데, 이를 잘 구분해주어야 한다. 안그러면, 결과값에 영향을 많이 미치기 때문이다.

 

0. 인자 (Class Variables)

---

두개의 함수에서는 variable 로 from_logits 과 reduction 을 주게 되는데 이에 대해서 알아보자.

1. from_Logits

- Keras API 에서는 from_Logits값이 Default(기본값)으로 False가 되어있습니다. 자 그럼 이 인자가 무슨 역활인지 알아봅시다. model 의 출력값이 are not normalized 되었을때, From_logits = True 라고 명시를 하고 있다. 이 말인 즉슨, 출력값을 보통 softmax, sigmoid 등등으로 normalize 해주게 되는데, 이를 적용시켜주었으면, False(default 값) 적용이 안되었다면 True 의 값을 나타낸다.

- 다음과 같이 소프트 맥스 함수를 보게되면 , \(y_{k}\) 값은 다 더하면 1 즉 , 확률값으로 표현되었다는 것을 알수있다.

 

- 좀 쉽게 말하자면, 우리가 출력층에 softmax, sigmoid든 무슨 함수를 적용시켜서 확률값으로 변형시켜주었으면,곧 확률값 함수로 변형되었기에 우리의 From_Logits = False 로 설정되어서, 값이 출력된다는 것이다. 그럼 확률값으로 변형되었을때, 어떻게 처리가 될까 하니..

if not from_logits:
    if (isinstance(output, (ops.EagerTensor, variables_module.Variable)) or
        output.op.type != 'Softmax'):
      epsilon_ = _constant_to_tensor(epsilon(), output.dtype.base_dtype)
      output = clip_ops.clip_by_value(output, epsilon_, 1 - epsilon_)
      output = math_ops.log(output)
    else:
      # When softmax activation function is used for output operation, we
      # use logits from the softmax function directly to compute loss in order
      # to prevent collapsing zero when training.
      # See b/117284466
      assert len(output.op.inputs) == 1
      output = output.op.inputs[0]
      # 참고 https://github.com/tensorflow/tensorflow/blob/

- 여기서 보면 from_logits = False 일때(default 값 = 확률값으로 표시 되었을때 = 출력층 함수가 설정 되었을때), 이 구문이 실행되는데, 이는 output 의 값(여기서 output은 Categorical_crossentrophy 함수가 받는 label 이 아닌 output 즉 우리의 model 이 예측한 값) 이 epsilon 에서 1-epsilon의 범위와 log 형식으로 바뀌는 것을 볼 수 있다. 이 부분을 떼와서 함수로 출력해보면,

from_logits = False 일때 값이 어떻게 바뀌는가.

- 다음 과 같이 나름의 log 값으로 변형시켜서 값들을 출력해준다.

 

- 그럼 이제 From_logits = True 일때와 False 일때 얼마나 차이나는지 비교해보자.

 

1. From_logits =  False(default 값일때)

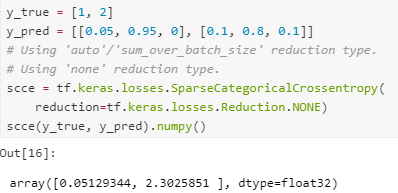
[From_logits = True]

-From_logits = False 일때 값이 array([0.05129344, 2.3025851 ], dtype=float32) 로 변환되어 나왔고,

 

2. From_logits =  True 일때

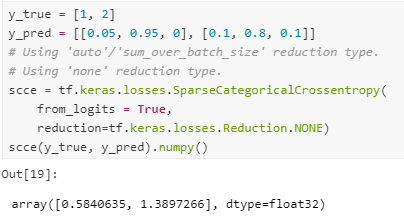
-From_logits = True 일때 값이 array([0.5840635, 1.3897266], dtype=float32) 로 변환되어 나왔다. 

 

- 결론) 결과값이 많이 차이나는 것을 볼 수 있다. 우리가 보통 층에 sigmoid 등등 의 함수를 출력값 함수로 넣기 때문에 from_logits = Fale(default 값) 가 되어서 문제는 발생하지 않을 것이다. 하지만, default 값이 True 가 될때에는 값이 많이 튀게 되니 조심해서 사용해주자.

 

그럼 이제 Reduction 에 대해 간단히 알아보자.

2. reduction 

- reduction 은 단순히 그 값을 값 각자에 집어넣은 값을 반환해주느냐, 아니면 합쳐서 반환해주느냐의 차이이다.

reduction = tf.keras.losses.Reduction.SUM 일때

reduction = tf.keras.losses.Reduction.SUM 으로 설정해주게 되면, 다음과 같이 그 값들이 합해져서 나오게 되고, 이는 곧 default 값이다. 그냥 각자 나오는 값을 원한다면, reduction =tf.keras.losses.Reduction.NONE 을 써주면 된다.

 

 

 

 

 

 

1. Categorical_crossentrophy

---

- Categorical_crossentrophy 와 같은 경우, one-hot-encoding이 된 결과로 나온 값들로 구성된다. 따라서, 우리가 비교하고자 하는 label값이 one-hot-encoding 되있는 상태여야 한다는 것이다.

y_true = [[0, 1, 0], [0, 0, 1]]
y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]]
# Using 'auto'/'sum_over_batch_size' reduction type.  
cce = tf.keras.losses.CategoricalCrossentropy()
#결과값
cce(y_true, y_pred).numpy()
1.177

- 수학식 \(L = \sum_{j}t_{i,j}log(pi,j)\)

- 따라서 위의 경우 \(log(0.95) + 0.1*log(0.1)\) 이 된다. 기본 sum method를 사용한다.

- 아래는 텐서플로우 categorical_crossentrophy 에서 사용하는 theano.nnet의 기본 method 이다.

def categorical_crossentropy(coding_dist, true_dist):
    # coding_dist, true_dis 두개의 인자를 받아서 차원이 같으면
    if true_dist.ndim == coding_dist.ndim:
    	아래의 수학공식을 그대로 적용하는 것을 볼 수 있다. 기본 sum 으로 반환
        return -tensor.sum(true_dist * tensor.log(coding_dist),
                           axis=coding_dist.ndim - 1)
    elif true_dist.ndim == coding_dist.ndim - 1:
        return crossentropy_categorical_1hot(coding_dist, true_dist)
    else:
        raise TypeError('rank mismatch between coding and true distributions')

- ex) model.compile(optimizer=.., loss='categorical_entropy')

 

2. Sparse_categorical_crossentrophy

---

- 똑같이 손실함수로 쓰이지만, 비교하는 값이 int type 이라는 것이다. 따라서 실측 label 값이 우리가 흔히 보는 [1] 과 같은 label 의 형태를 띄고 있어도 된다는 것이다. 쉽게 예를 들어 fashion-mnist 의 label 은 원핫인코딩 되있는 상태가 아닌 단순 숫자형(int dtype) label 이다 . 

 

- 따라서 손실함수로 주었을때, Sparse_categorical_crossentrophy를 주어야지, Categorical_crossentrophy를 주게되면, shape 에러가 나오게 된다.

 

y_true = [1, 2]
y_pred = [[0.05, 0.95, 0], [0.1, 0.8, 0.1]]
loss = tf.keras.losses.sparse_categorical_crossentropy(y_true, y_pred)
assert loss.shape == (2,)
loss.numpy()

# 결과값
array([0.0513,2.303], dtype = float32)

 

- 진짜 sparse_categorical_crossentrophy 는 어떻게 계산하는지 궁금해서 찾아보는데 안나와서 github 가서 뒤져온 source~ 인데,,, 첨가는 안했다. 결론은 뒤에..

 

- 진짜 간단히 말하자면, 밑의 코드는 tensorflow.keras 에 있는 모듈인데, 데이터 전처리를 해준다음, tf.backend 의 sparse_categorical_crossentrophy 로 다시 계산해준다.

def sparse_categorical_crossentropy(y_true, y_pred, from_logits=False, axis=-1):
  # 우선 tensor 로 변환시켜주고~
  y_pred = tf.convert_to_tensor(y_pred)
  # y_true 를 y_pred 와 같은 dtype으로 변경시켜준다.
  y_true = tf.cast(y_true, y_pred.dtype)
  return backend.sparse_categorical_crossentropy(
      y_true, y_pred, from_logits=from_logits, axis=axis)

- 근데 결국 뒤지다 보니 똑같은 함수를 사용한다.. 하하

- 둘다 cross_entrophy 함수를 사용하고, 그치만 sparse_categorical_crossentropy 함수는 one-hot encoding 을 안하다 보니, 메모리 소요가 적다는 장점이 있는 걸로 알고 넘어가면 되겠다.

 

 

3. 직접 구현 (Sparse_categorical_crossentrophy)

---

- 설명은 각 주석을 통해 달았으니 참고하자. 

- 처음에, one_hot_encoding 후, softmax 함수로 확률값으로 변형 후, 끝에 \(L = \sum_{j}t_{i,j}log(pi,j)\) 식을 적용시켜서 최종식을 완성하였다.

logits = tf.constant([[-3.27133679, -22.6687183, -4.15501118, -5.14916372, -5.94609261,
                       -6.93373299, -5.72364092, -9.75725174, -3.15748906, -4.84012318],
                      [-11.7642536, -45.3370094, -3.17252636, 4.34527206, -17.7164974,
                      -0.595088899, -17.6322937, -2.36941719, -6.82157373, -3.47369862],
                      [-4.55468369, -1.07379043, -3.73261762, -7.08982277, -0.0288562477, 
                       -5.46847963, -0.979336262, -3.03667569, -3.29502845, -2.25880361]])
labels = tf.constant([2, 3, 4])

# logits 를 각 함수가 예측한 값 즉, from_logits = True로 적용되어야함.
loss_object = tf.keras.losses.SparseCategoricalCrossentropy(
    from_logits=True, reduction='none')
loss = loss_object(labels, logits)
print(f'{loss.numpy()}\n{tf.math.reduce_sum(loss).numpy()}')
''' 예측값
loss.numpy() : [2.0077198  0.00928146 0.6800677 ]
tf.math.reduce_sum(loss).numpy() : 2.697068929672241
'''

# 우선 one_hot_labeling을 시켜준다.
one_hot_labels = tf.one_hot(labels, 10)
'''
<tf.Tensor: shape=(3, 10), dtype=float32, numpy=
array([[0., 0., 1., 0., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 1., 0., 0., 0., 0., 0., 0.],
       [0., 0., 0., 0., 1., 0., 0., 0., 0., 0.]], dtype=float32)>
'''

# multi label 이므로 softmax함수를 그대로 적용시켜서, 확률값으로 변경해준다.
preds = tf.nn.softmax(logits)
'''
<tf.Tensor: shape=(3, 10), dtype=float32, numpy=
array([[0.08533674, 0.08533674, 0.23196931, 0.08533674, 0.08533674,
        0.08533674, 0.08533674, 0.08533674, 0.08533674, 0.08533674],
       [0.08533674, 0.08533674, 0.08533674, 0.23196931, 0.08533674,
        0.08533674, 0.08533674, 0.08533674, 0.08533674, 0.08533674],
       [0.08533674, 0.08533674, 0.08533674, 0.08533674, 0.23196931,
        0.08533674, 0.08533674, 0.08533674, 0.08533674, 0.08533674]],
      dtype=float32)>
'''
preds /= tf.math.reduce_sum(preds, axis=-1, keepdims=True)
# crossentropy 값은 label 된 확률값에 -log() 취해주어 값을 더해준다. 
loss = tf.math.reduce_sum(tf.math.multiply(one_hot_labels, -tf.math.log(preds)), axis=-1)
print(f'{loss.numpy()}\n{tf.math.reduce_sum(loss).numpy()}')
''' 손으로 구현 한 값
loss.numpy() : [2.0077198  0.00928146 0.6800677 ]
tf.math.reduce_sum(loss).numpy() : 2.697068929672241
'''

공부도 많이하고 정리를 해봤는데,, 큰 도움이 되었으면 합니다~