정규 분포 (Gaussian Distribution)

0. 서론

---

- 정규분포는 18세기 후반 과 19세기 초반의 위대한 독일의 수학자 카를 프리드리히 가우스이 이름을 따 가우스 분포 Gaussinan_Distribution 이라고도 불리는데, 다음과 같은 공식을 따른다.

1. 단일 변수의 가우시안 정규 분포

 

1. 공식

---

1. 단일 변수의 가우시안 정규 분포

가우시안 정규분포를 그려보게 되면 다음과 같은 형태를 띄게 된다.

from numpy import random
import seaborn as sns
sns.distplot(random.normal(size=1000), hist=False)
plt.show()

 

 

2. 정규분포의 정규화(Normalized) 확인

---

- 정규분포가 정규화 즉, 다음을 만족시키는지 확인해보자.

 

 

- 제일 간단한 형태부터 시작하기 위해서 \( u = 0 \), 즉 평균은 0일 때부터 확인해보자.

 

- \( u = 0\) 을 만족시킬때, 정규분포의 형태는 \( I = \int_{-\infty}^{\infty} exp(-\frac{1}{2\sigma^2} x^2) dx\) 이 되게 되고, 이를 풀어주기 위해서 \( I = \int_{-\infty}^{\infty} exp(-\frac{1}{2\sigma^2} x^2) dy\) 의 적분을 한 번 더 씌워주게 되면, 

 

- \( I^2 = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \exp(-\frac{1}{2\sigma^2}(x^2+y^2)) dx dy\)  가 되게 되고, 여기서 \( x^2 + y^2 = r^2 \) 으로 치환해주면, 

 

- 다음과 같은 계산식을 따르게 된다. 따라서

 

- 결국 \( \int_{-\infty}^{\infty} \sigma^2 d\theta = 2\pi\theta^2 \) 이 되게 된다. 따라서 우리가 구하고자 했던 값  \( I = \sqrt{2\pi\theta^2} \) 이  최종적으로 만족시키게 된다.

 

- 결론적으로 앞에 있던 \( \frac{1}{\sqrt{2\pi\theta^2}} \) 와 없어지면서 정규화를 만족시키게 된다.

from numpy import random
from scipy.stats import norm
fig,ax = plt.subplots()

x = np.linspace(-10,10)
ax.plot(x,norm.pdf(x))
ax.set_title("Gaussian Distribution")
ax.set_xlabel("x")
ax.set_ylabel("pdf(x)")

lx= np.arange(-10,0,0.01)
ax.fill_between(px,norm.pdf(lx),alpha = 0.3, color = "g")
rx= np.arange(0,10,0.01)
ax.fill_between(rx,norm.pdf(rx),alpha = 0.3, color = "r")

ax.text(-2,0.02,round(norm.cdf(x=0),1), fontsize = 15)
ax.text(0.3,0.02,round(1-norm.cdf(x=0),1), fontsize = 15)
plt.show()

- 좌측과 우측에 Norm.cdf(x = ) 로 각 확률값을 표현하였다.

 

 

3. 정규분포의 기댓값( Expectation of Gaussian Distribution)

---

- 정규분포의 기댓값과 분산 은 다음과 같은 과정을 통해 우리가 알고 있던 \( u \) 와 \( \theta\) 가 나오는 것을 확인 가능하다.

정규분포의 기댓값 계산식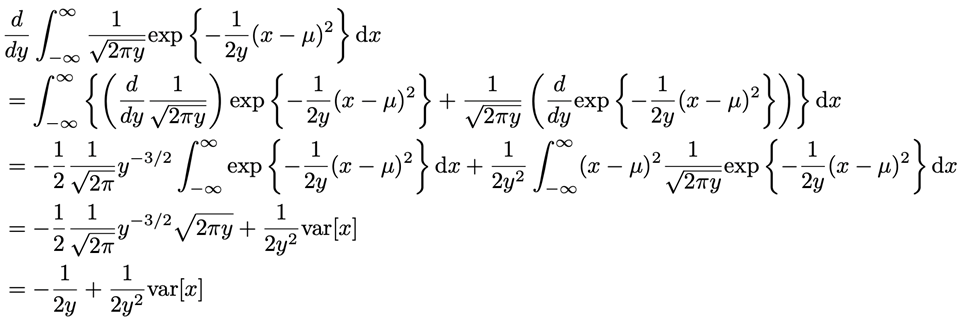

정규분포의 분산 계산식

 

- 여기서 당연히 평균이랑 분산값을 \( u \) 와 \( \theta\) 로 했으니 같은 값나오는게 아니냐 하실텐데, 설정된 \( u \) 와 \( \theta\) 의 값을 정규분포(Gaussian Distribution) 에 넣고, 계산을 했을때,

 

- 즉, \( E[f] = \int_{}{} p(x)f(x) dx\) 를 하였을시, 기댓값이 \(u\) 그리고 표준편차가 \( \theta\) 가 나오는 것을 한번더 확인 한 것이다.

 

 

 

 

 

4. 정규분포의 최대 우도 해(Maximum Likelihood solution)

---

- 먼저 우도(Likelihood) 란? 나타난 결과에 따라 여러 가능한 가설들을 평가할 수 있는 측도(Measure)로써, 최대 우도해(Maximum Likelihood solution) 은 여러 가능한 가설중 일어날 가능성이 가장 큰 우도이다. 

 

- 쉬운 예를 들자면, 동전을 앞뒤로 던지는 시뮬레이션을 할때, 앞면이 얼마에 한번 나오는지 모르는 상황이라고 하자. 그럴때, 시뮬레이션을 1000번 정도해서, 앞이 500번 뒤가 500번 나왔을때, 우리는 직감적으로 가설의 최대우도해 는 0.5,0.5 인 것을 알 수 있다.

 

- 그렇다면 HOW?? 어떻게 최대우도해를 구하나.?

 

- 해의 분포는 : 평균이 \( u_{ml} = \frac{1}{N} \sum_{n=1}^{N}x_{n} \) 그리고 표준편차가 \(\sigma_{ML}^{2} = \frac{1}{N}\sum_{n=1}^{N}(x_{n}-u_{ML})^2\) 을 만족시키게 되는 정규분포를 따른다.

 

- 이를 증명해보자. 

 

- 우선 \( X = (x_{1}, x_{2}, ... , x_{n})^{T} \) 의 독립적인  N개의 샘플들이 있고, 각 \( x_{1}, x_{2}, ... , x_{n} \) 의 샘플들이 가우시안 분포(= 정규분포) 로부터 추출되었다 하자.

 

 

 

 

- 4.1 최대 우도해의 평균(\( u_{ml} = \frac{1}{N} \sum_{n=1}^{N}x_{n} \)) 증명

---

- \(p(X|u,\sigma^{2}) = p(x_{1}, x_{2}, ... , x_{n}| u,\sigma^{2}) = \prod_{1}^{N} N(x|u,\sigma^{2}) \) 를 만족시키고,

 

- 이식에다가 \(ln \) 을 씌워주어서, 곱하기를 모두 더해주는 것으로 내려주면, 최종식은 

- 다음과 같이 된다. 이때, 최대 우도해가 되려면 \( \frac{d}{du} ln p(X|u,\sigma^{2})\) 가 0이 될때 최대 값을 가지므로, 미분을 진행한 식은 다음과 같고,

- 여기서 \((\sum_{n=1}^{N}x_{n}) - Nu = 0\) 을 만족시키므로, 평균값 \( u_{ML} \)은 다음을 만족시킨다.

 

 

 

 

- 4.2 최대우도해의 분산(\(\sigma_{ML}^{2} = \frac{1}{N}\sum_{n=1}^{N}(x_{n}-u_{ML})^2\) )증명 

---

- 앞서 말한 \(ln\) 으로 정리된 식을 다시 불러오면,

- 여기서 최대값을 가지는 우도해의 분산은 분산으로 미분해주었을때, 0이 되는 분산값을 구해주면 되고, 구하기에 앞서 \( y = \sigma^{2} \) 으로 치환해준다.

 

- \( y\) 으로 미분해주면 다음과 같이 되고, 

 

- 여기서 \( \frac{1}{2}y^{-1} \) 을 빼주게 되어 정리해주면, 우리가 원하는 분산 \( \sigma^{2}\) 는 이렇게 정리된다.