신경망(Neural_Net) 에서의 선형변환(Linear_Transform) 및 어파인 변환

1. 선형변환의 기하학적 의미

---

저번 포스팅에서도 보았듯이, 선형변환은 f(v1 + v2) = f(v1) + f(v2) 로 표현이 된다 했었는데, 이를 벡터공간으로 바라보게 된다면,

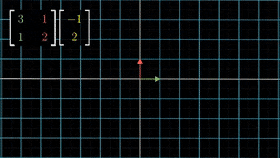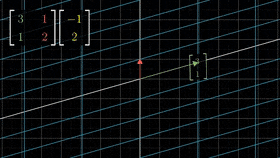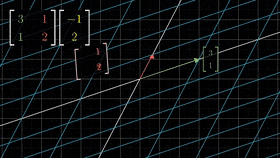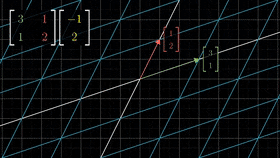
linear transformaion 을 나타낸 그림[1].

linear transformaion 을 나타낸 그림[2].

 

- 그림 [1] 에서는 [1,0] 과 [0,1] 의 격자벡터가 [3,1]과 [1,2] 로 나타내어지는 것을 볼 수 있다.

- 그림 [2] 에서는 각 격자들이 선형변환이 될 떄 어떻게 움직이는지를 말해준다.

 

여기서 볼 수 있듯이, 선형변환을 하게 되면, 격자들이 선형변환이 된 후 에도, 선의 형태(Linear)하게 움직였다는 것이고, 격자들의 간격 또한 Linear 하게 펼쳐 졌다. (같은 차원에서의 변환이지만, 차원이 다를때에도 마찬가지이다.) 하지만, 우리가 보는 Neural Net 에서의 선형변환으로는 더 복잡한 표현들이 불가능하다. 

예를 들면,

neural net 의 격자변환을 나타내는 그림[3].

이 처럼 복잡하게 구부러진 변환들은 단지 선형변환(Linear Transformation) 으로는 표현이 불가능하다. 따라서 신경망 학습 모델은 Bias 와 ReLU 함수등을 통하여, 격자모형에 변환을 주어, 원하는 형태의 변환이 가능토록 하는 것이다. 이제부터는 각 단계별로 신경망 학습 모델들을 설명하겠다.

 

 

 

 

 

2. 선형 변환 (Linear Transform) 의 단계

---

- Linear Transform 의 단계에서는 격자들이 선형변환 을 띄고 일정한 간격을 두고 이동하게 된다. 

Linear Transform [그림 4]

다음과 같이 격자들이 선형변환을 띄면서 격자가 선형변환 된 크기 만큼 늘려진다.

 

3. Bias Transform 의 단계

---

 

-2번 째 단계로 Bias 들에 의해 격자들이 움직이게 된다.

bias 로 인한 transformation 그림[5]

4. NonLinear Transform 의 단계

---

- 3 번째 단계로 이 격자들이 바깥쪽으로 가게 되었을 때 , Shrink하게 되는데, 이는 오차들이 전파 되면서, 오차가 0 보다 엄청 크게 되는 부근에서는 왜곡이 되어, 격자의 무늬가 쭈글어들게 된다.

.Shrink 되는 격자들 그림[6]

 이와 같이 Neural net 에서는 단순히 선형회귀 만으로는 데이터들에게 맞는 신경망을 학습시킬 수 없기 때문에, 여러가지를 조합하여 Neural Net 을 학습하게 된다. 이런식으로 신경망이 Visualization 을 시켰는데, 아무쪼록 이해가 잘 되었으면 하는 바램이다. 

 

 

 

5. ref.

---

1. Neural Networks, Manifolds, and Topology -- colah's blog

Neural Networks, Manifolds, and Topology -- colah's blog

2. www.boostcourse.org/ai251

인공지능을 위한 선형대수

 

- 잘 보셨으면, 댓글 부탁드립니다~ ㅎㅎ